

The above definitions are equally valid for a pseudo-Riemannian metric. In short, the expression you provided holds locally for an inertial coordinate system with a timelike coordinate and three space-like coordinates. where are the Christoffel symbols of the metric, and is the partial derivative of in the -coordinate direction.
In carved spacetimes lin particular also for the FRW metric) it is. Nevertheless, the existence of the four-potential $A_\mu$ is also only ensured locally. This defines the Christoffel symbol I, that apparently vanishes in Cartesian coordinates. On an inertial coordinate system with one time component and three spatial components, the Christoffel symbols vanish and this equation reduces to the usual expression, so your formula is valid, but only locally. $$F_ = \nabla_\mu A_\nu - \nabla_\nu A_\mu$, where $\nabla_\mu$ is the covariant derivative. In other words, a freely moving or falling particle always moves along a geodesic. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. The electromagnetic field tensor defined with covariant derivatives or with standard partial derivatives is the same simply due to the anti-symmetry of this tensor: In general relativity, a geodesic generalizes the notion of a 'straight line' to curved spacetime.
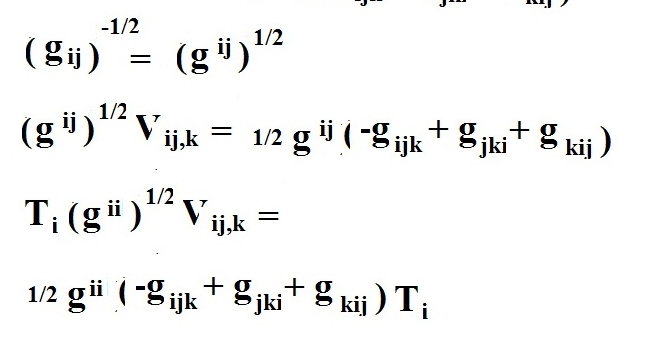
Actually, the things are easier than you might think.


 0 kommentar(er)
0 kommentar(er)
